E' vero che aumentando il perimetro aumenta pure l'area?

Il numero più grande

In sei foglietti ci sono scritti rispettivamente i seguenti numeri: 309 - 41 - 5 - 7 - 2 - 68
Accostando tutti i sei foglietti puoi formare dei numeri di dieci cifre, ad esempio 6841309572. Qual è il più piccolo?

Questo esercizio all'inizio sembra, ed è, molto facile. Solo che qualcuno potrebbe fare ragionamenti che rendono impossibile la soluzione. Invece basta ragionare sulle prime cifre di ogni numero. Prendendo in considerazione la cifra più piccola "2" e continuando col "3" del numero 309 fino al numero "7". Il numero sarà il seguente: 2309415687!
Andrea Calderone

Simmetria in natura

Sbirciando negli altri blog della nostra scuola ho visto una foto che mi è piaciuta molto!

Eccola





La foto, fatta dalla dott.ssa Zanghì, docente nel corso di scienze rivolto ai bambini della scuola primaria, ha stuzzicato la mia curiosità... ho voluto verificare se era possibile trovare un asse di simmetria. Di seguito il risultato (con geogebra)


L'immagine è il risultato della sovrapposizione della foto originale con la simmetrica. Cosa ne pensate? Come possiamo giustificare il fatto che una parte sembra più grande dell'altra?
Leggerò con estremo piacere ed interesse i vostri commenti

Somma dei primi 100 numeri, costruzione geometrica

Riporto da :http://www.vialattea.net/esperti/mat/sq/



... La leggenda vuole che a scoprirla sia stato il genio di Gauss, in tenera età, grazie ad una elegante intuizione geometrica. Si osservi la figura 1:

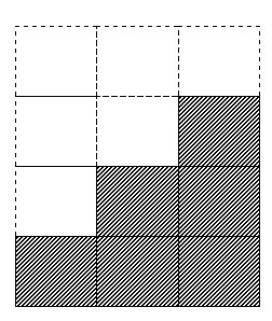
Fig. 1: La somma dei primi n naturali è pari alla semiarea del rettangolo di lati n ed n+1

La chiave risolutiva è l’osservazione che il numero di quadrati tratteggiati (ovvero la somma dei primi 3 numeri naturali) è pari alla semiarea del triangolo di lati 4 e 3. ...

Caccia all'errore

Mi riferisco al post di Pierpaolo....
vediamo , se seguo le sue istruzioni non mi sembra che il risultato sia 5050 bensì 510050!!! Vi chiedo (o ordino?) poichè Pierpaolo, preso dalla foga di parlar male della sua prof di mate (chi sarà mai?), ha esplicitato male le operazioni da fare, chi è in grado di trovare l'errore e correggerlo?
Il capo
p.s. certamente avrei preferito fare le stesse cose di Gauss anzichè quelle del suo prof di mate... cmq meglio che niente...

Somma dei primi 100 numeri

Un giorno la professoressa di matematica, crudelmente, ci ha chiesto (ordinato) di trovare il risultato della somma dei primi 100 numeri. Dopo circa un quarto d'ora di esaurimento nervoso, la prof ci ha spiegato il trucco: dovevamo sommare il primo numero con l'ultimo, il secondo con il penultimo e così via e potevamo vedere che la somma veniva sempre 101 e poi dovevamo dividere per 2/100 e poi moltiplicarlo per 101 e il risultato è 5050. Questo mi è servito da lezione perchè lo stesso esercizio mi è stato proposto nelle gare dell'A.I.C.M.
Pierpaolo Letizia

Auguriiiii!!!!!!

Vi piace di più così?
Datemi suggerimenti per migliorare il nostro blog e... commentate!
Il capo

Benvenuti!

Cominciamo oggi questo percorso insieme, guidati dal prof. Gentile.
Mentre io scrivo, voi siete concentrati e divertiti come mai in classe.... che invidia!!!
Questo blog è il nostro diario di bordo, qui racconterete, commenterete, condividerete.... ecc... tutto ciò che vorrete che sia attinente al corso che state seguendo.
Cominciamo subito:
prima domanda del test (ahah vi siete fatti fregare!!!):
qual è il successivo di 2,37?
Prego, cominciate a spiegarmi questa cosa commentando questo post.
Il capo